Understanding Cryptography by Christof Paar and Jan Pelzl - Chapter 1 Solutions - Ex1.12
- 2 mins- Return to index
- Exercise 1.1
- Exercise 1.2
- Exercise 1.3
- Exercise 1.4
- Exercise 1.5
- Exercise 1.6
- Exercise 1.7
- Exercise 1.8
- Exercise 1.9
- Exercise 1.10
- Exercise 1.11
- Exercise 1.12
- Exercise 1.13
- Exercise 1.14
Exercise 1.12
Now, we want to extend the affine cipher from Sect. 1.4.4 such that we can encrypt and decrypt messages written with the full German alphabet. The German alphabet consists of the English one together with the three umlauts, Ä, Ö, Ü, and the (even stranger) “double s” character ß. We use the following mapping from letters to integers:
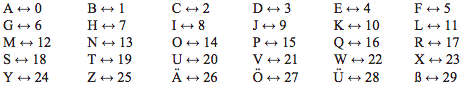
- What are the encryption and decryption equations for the cipher?
- How large is the key space of the affine cipher for this alphabet?
- The following ciphertext was encrypted using the key (a = 17, b = 1). What is the corresponding plaintext?
- From which village does the plaintext come?
Solution
This decryption part of the solutions (1. and 3.) are verified as correct by the fact that they produce sensible output. If you can see an error in my reasoning for 2. then please leave a comment in the Disqus box below.
1. The encryption and decryption functions are defined as follows:
\[e_k(x) = y \equiv a ⋅ x + b\,\mathrm{mod}\,30\] \[d_k(y) = x \equiv a^{-1} ⋅ (y - b)\,\mathrm{mod}\,30\] \[\mathsf{where}\, k = (a, b)\,\mathsf{such\,that}\,\mathrm{gcd}(a, 30) = 1\]2. The keyspace is defined as the cartesian product of the possible \(a\) values and the possible \(b\) values. \(a\) needs to be co-prime with 30 in order for it to have a multiplicative inverse in \(\mathbb{Z}_{30}\). As such the number of possible \(a\) values is \(\phi(30) = 8\). Since \(b\) can be any value in \(\mathbb{Z}_{30}\) (beacause 0 still performs encryption) then the number of possible b values is 30.
As such the number of total keys is \((8 \times 30) - 1 = 239\). We subtract 1 from the total in order to eliminate \((1, 0)\) since that key doesn’t perform encryption.
3. When using the key \((17, 1)\), this is the result of decryption:
\[d_k(ä, u, ß, w, ß) = FRODO\]4. Frodo comes from The Shire.
Thomas Busby
I write about computing stuff