Understanding Cryptography by Christof Paar and Jan Pelzl - Chapter 1 Solutions - Ex1.1

Saturday. 16 December 2017 - 6 mins

Exercise 1.1

The ciphertext below was encrypted using a substitution cipher.

Decrypt the ciphertext without knowledge of the key.

lrvmnir bpr sumvbwvr jx bpr lmiwv yjeryrkbi jx qmbm wi bpr xjvni mkd ymibrut jx irhx wi bpr riirkvr jx ymbinlmtmipw utn qmumbr dj w ipmhh but bj rhnvwdmbr bpr yjeryrkbi jx bpr qmbm mvvjudwko bj yt wkbrusurbmbwjk lmird jk xjubt trmui jx ibndt

wb wi kjb mk rmit bmiq bj rashmwk rmvp yjeryrkb mkd wbi iwokwxwvmkvr mkd ijyr ynib urymwk nkrashmwkrd bj ower m vjyshrbr rashmkmbwjk jkr cjnhd pmer bj lr fnmhwxwrd mkd wkiswurd bj invp mk rabrkb bpmb pr vjnhd urmvp bpr ibmbr jx rkhwopbrkrd ywkd vmsmlhr jx urvjokwgwko ijnkdhrii ijnkd mkd ipmsrhrii ipmsr w dj kjb drry ytirhx bpr xwkmh mnbpjuwbt lnb yt rasruwrkvr cwbp qmbm pmi hrxb kj djnlb bpmb bpr xjhhjcwko wi bpr sujsru msshwvmbwjk mkd wkbrusurbmbwjk w jxxru yt bprjuwri wk bpr pjsr bpmb bpr riirkvr jx jqwkmcmk qmumbr cwhh urymwk wkbmvb

Compute the relative frequency of all letters A…Z in the ciphertext. You may want to use a tool such as the open-source program CrypTool [50] for this task. However, a paper and pencil approach is also still doable.
Decrypt the ciphertext with the help of the relative letter frequency of the English language (see Table 1.1 in Sect. 1.2.2). Note that the text is relatively short and that the letter frequencies in it might not perfectly align with that of general English language from the table.
Who wrote the text?

Solution

This solution is verified as correct by the official Solutions for Odd-Numbered Questions manual.

1. Tallying up the letter frequencies produces the table below:

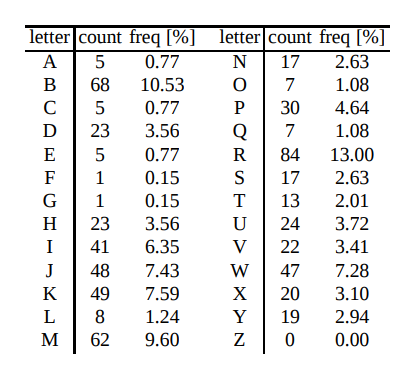
Frequency table

2. Pairing this frequency table with the list of most common letters in the English language does not yield a key which produces intelligible text. However, enough words “stick out” that it’s fairly simple to swap mismatches manually until the plaintext reveals itself:

BECAUSE THE PRACTICE OF THE BASIC MOVEMENTS OF KATA IS THE FOCUS AND MASTERY OF SELF IS THE ESSENCE OF MATSUBAYASHI RYU KARATE DO I SHALL TRY TO ELUCIDATE THE MOVEMENTS OF THE KATA ACCORDING TO MY INTERPRETATION BASED ON FORTY YEARS OF STUDY

IT IS NOT AN EASY TASK TO EXPLAIN EACH MOVEMENT AND ITS SIGNIFICANCE AND SOME MUST REMAIN UNEXPLAINED TO GIVE A COMPLETE EXPLANATION ONE WOULD HAVE TO BE QUALIFIED AND INSPIRED TO SUCH AN EXTENT THAT HE COULD REACH THE STATE OF ENLIGHTENED MIND CAPABLE OF RECOGNIZING SOUNDLESS SOUND AND SHAPELESS SHAPE I DO NOT DEEM MYSELF THE FINAL AUTHORITY BUT MY EXPERIENCE WITH KATA HAS LEFT NO DOUBT THAT THE FOLLOWING IS THE PROPER APPLICATION AND INTERPRETATION I OFFER MY THEORIES IN THE HOPE THAT THE ESSENCE OF OKINAWAN KARATE WILL REMAIN INTACT

3. This was said by Shoshin Nagamine.

I wrote a python script which can perform this frequency analysis attack:

import collections, re

def get_ciphertext_letters_by_frequency(ciphertext):
    ciphertext_nopunc = re.sub(r"\W+", "", ciphertext)
    letter_freqs = collections.Counter(ciphertext_nopunc)
    return [i[0] for i in letter_freqs.most_common()]

def reconstruct_key(ciphertext_letters):
    letters_ordered_by_freq = ["E","T","A","O","I","N","S","R","H","D","L",
        "U","C","M","F","Y","W","G","P","B","V","K","X","Q","J","Z"]
    return zip(ciphertext_letters, letters_ordered_by_freq)

def get_manually_tweaked_key():
    # The statistical analysis produced a plaintext that was still garbled
    # but certain words stood out. I swapped these mismatches manually until
    # the true plaintext revealed itself. This was very easy given the
    # headstart provided by the statistical analysis
    return [
        ('r', 'E'), ('b', 'T'), ('m', 'A'),
        ('k', 'N'), ('j', 'O'), ('w', 'I'),
        ('i', 'S'), ('p', 'H'), ('u', 'R'),
        ('d', 'D'), ('h', 'L'), ('v', 'C'),
        ('x', 'F'), ('y', 'M'), ('n', 'U'),
        ('s', 'P'), ('t', 'Y'), ('l', 'B'),
        ('o', 'G'), ('q', 'K'), ('a', 'X'),
        ('c', 'W'), ('e', 'V'), ('g', 'Z'),
        ('f', 'Q')
    ]

def decipher(ciphertext, key):
    for x, y in key:
        ciphertext = ciphertext.replace(x, y)
    return ciphertext

def print_ciphertext(ciphertext):
    print "\n==========="
    print "Ciphertext:"
    print "==========="
    print ciphertext

def print_deciphered_plaintext(type, key, plaintext):
    header = "{} Statistical Key Reconstruction:".format(type)
    print "=" * len(header), "\n", header, "\n", "=" * len(header)
    print "\n", "Key:", "\n"
    key.sort(key=lambda x: x[1])
    i = 0
    for x, y in key:
        print "{} = {},".format(y, x),
        i += 1
        if not i % 5: print
    print "\n", plaintext

with open("ex1.1-ciphertext.txt") as f:
    ciphertext = f.read()
    print_ciphertext(ciphertext)
    ciphertext_letters = get_ciphertext_letters_by_frequency(ciphertext)
    key = reconstruct_key(ciphertext_letters)
    print_deciphered_plaintext("Naive", key, decipher(ciphertext, key))
    key = get_manually_tweaked_key()
    print_deciphered_plaintext("Manually Tweaked", key, decipher(ciphertext, key))
    print "Q1.1.3 Answer: This was said by Shoshin Nagamine", "\n"

Previous Exercise Next Exercise

Thomas Busby

I write about computing stuff