Understanding Cryptography by Christof Paar and Jan Pelzl - Chapter 2 Solutions - Ex2.10

Tuesday. 19 December 2017 - 3 mins

Exercise 2.10

We conduct a known-plaintext attack on an LFSR-based stream cipher. We know that the plaintext sent was:

1001 0010 0110 1101 1001 0010 0110

By tapping the channel we observe the following stream:

1011 1100 0011 0001 0010 1011 0001

What is the degree $m$ of the key stream generator?
What is the initialization vector?
Determine the feedback coefficients of the LFSR.

Solution

This solution is verified as correct by the fact that it produces sensible output which can be fed back in for confirmation.

1. By XORing the ciphertext stream with the keystream, we get the following:

0010 1110 0101 1100 1011 1001 0111

If we arrange this into 7 bit blocks then we can easily see that the key repeats every 7 bits. The period of the LFSR is therefore 7.

0010111 0010111 0010111 0010111

Since the period of an LFSR (with primitive polynomial) is defined by $p = 2^m - 1$, we can rearrange this to $m = \log_2 (p + 1)$:

\[\log_2 (7 + 1) = 3\]

Therefore the degree of the LFSR must be 3.

2. The first $m$ bits of the keystream are $(s_0 = 0, s_1 = 0, s_2 = 1)$, so therefore the initialisation vector must be:

\[(s_2 = 1, s_1 = 0, s_0 = 0)\]

3. Using the following 3 bits of the keystream (since we require $2m$ key bits for an attack), we can construct a set of simultaneous equations where the unknowns are the feedback coefficients that produced those next three values:

\[s_2p_2 + s_1p_1 + s_0p_0 = s_3\] \[s_3p_2 + s_2p_1 + s_1p_0 = s_4\] \[s_4p_2 + s_3p_1 + s_2p_0 = s_5\]

Using our specific values, we get the following:

\[1p_2 + 0p_1 + 0p_0 = 0\,(s_3)\] \[0p_2 + 1p_1 + 0p_0 = 1\,(s_4)\] \[1p_2 + 0p_1 + 1p_0 = 1\,(s_5)\]

This can be converted into an augmented matrix and solved via Gauss-Jordan Elimination:

$\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \end{array} \right]$

\[R_3 \rightarrow R_3 + R_1\]

$\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \end{array} \right]$

The matrix is now in reduced row echelon form, which allows the values of the unknowns to be read directly from the matrix. The feedback coefficients of the LFSR are $(p_0 = 1, p_1 = 1, p_2 = 0)$, which is represented graphically as follows:

LFSR

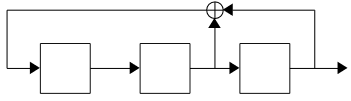
To double check that our solution is correct, we can run the reconstructed LFSR outselves to be sure that it produces the same keystream:

$\begin{array}{c|c c c|c} & s_2 & s_1 & s_0 & \text{Output} \\ \hline s_0 & 1 & 0 & 0 & 0 \\ s_1 & 0 & 1 & 0 & 0 \\ s_2 & 1 & 0 & 1 & 1 \\ s_3 & 1 & 1 & 0 & 0 \\ s_4 & 1 & 1 & 1 & 1 \\ s_5 & 0 & 1 & 1 & 1 \\ s_6 & 0 & 0 & 1 & 1 \\ \hline & 1 & 0 & 0 & 0 \end{array}$

Given that this LFSR outputs the same keystream, we have proved the correctness of our derived coefficients.

Previous Exercise Next Exercise

Thomas Busby

I write about computing stuff