Understanding Cryptography by Christof Paar and Jan Pelzl - Chapter 2 Solutions - Ex2.11

Tuesday. 19 December 2017 - 7 mins

Exercise 2.11

We want to perform an attack on another LFSR-based stream cipher. In order to process letters, each of the 26 uppercase letters and the numbers 0, 1, 2, 3, 4, 5 are represented by a 5-bit vector according to the following mapping:

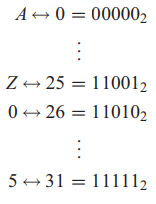
Mapping

We happen to know the following facts about the system:

The degree of the LFSR is $m = 6$.
Every message starts with the header WPI.

We observe now on the channel the following message (the fourth letter is a zero):

j5a0edj2b

What is the initialization vector?
What are the feedback coefficients of the LFSR?
Write a program in your favorite programming language which generates the whole sequence, and find the whole plaintext.
Where does the thing after WPI live?
What type of attack did we perform?

Solution

This solution is verified as correct by the official Solutions for Odd-Numbered Questions manual.

1. The first thing we need to do is convert the chosen plaintext “WPI” into binary:

10110 01111 01000

We next need the first three latters of ciphertext converted into binary:

01001 11111 00000

To extrapolate the keystream that encrypted our chosen plaintext, we simply XOR the two:

11111 10000 00100

Given that we know the degree of the LFSR is 6, then the first 6 bits of the keystream must be the initialisation vector:

2. To derive the feedback coefficients, we can exploit our knowledge of $2m$ bits of keystream:

$\begin{array}{c|c} s_{11} & s_{10} & s_9 & s_8 & s_7 & s_6 & s_5 & s_4 & s_3 & s_2 & s_1 & s_0 \\ \hline 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \end{array}$

The following simultaneous equations can be used to derive the feedback coefficients $p_i$:

\[s_5p_5 + s_4p_4 + s_3p_3 + s_2p_2 + s_1p_1 + s_0p_0 = s_6\] \[s_6p_5 + s_5p_4 + s_4p_3 + s_3p_2 + s_2p_1 + s_1p_0 = s_7\] \[s_7p_5 + s_6p_4 + s_5p_3 + s_4p_2 + s_3p_1 + s_2p_0 = s_8\] \[s_8p_5 + s_7p_4 + s_6p_3 + s_5p_2 + s_4p_1 + s_3p_0 = s_9\] \[s_9p_5 + s_8p_4 + s_7p_3 + s_6p_2 + s_5p_1 + s_4p_0 = s_{10}\] \[s_{10}p_5 + s_9p_4 + s_8p_3 + s_7p_2 + s_6p_1 + s_5p_0 = s_{11}\]

If we plug in our known values for $s_i$ then we can express this as the following augmented matrix and perform Gauss-Jordan Elimination:

$\left[ \begin{array}{cccccc|c} 1 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 \end{array} \right]$

\[R_1 \rightarrow R_1 + R_2\] \[R_2 \rightarrow R_2 + R_3\] \[R_3 \rightarrow R_3 + R_4\] \[R_4 \rightarrow R_4 + R_5\] \[R_5 \rightarrow R_5 + R_6\]

$\left[ \begin{array}{cccccc|c} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 \end{array} \right]$

The matrix is now in reduced row echelon form, and the values $p_i$ can be read directly from the matrix:

$\begin{array}{c|c} p_5 & p_4 & p_3 & p_2 & p_1 & p_0 \\ \hline 0 & 0 & 0 & 0 & 1 & 1 \end{array}$

3. I wrote a python script which can perform many of the operations involved in this attack:

Note: This is not a remotely efficient implementation of an LFSR-based Stream Cipher.

import string, re

def bit_encoding_map():
    return zip(string.ascii_lowercase + string.digits, range(0, 32))

def bitencode(text):
    def encode_char(c):
        map = dict(bit_encoding_map())
        return bin(map[c.lower()]).lstrip("-0b").zfill(5)
    return "".join([encode_char(c) for c in text])

def bitdecode(text):
    def decode_block(bits):
        map = dict([(b, a) for a, b in bit_encoding_map()])
        return map[int(bits, 2)].upper()
    return "".join([decode_block(bits) for bits in re.findall(".{1,5}", text)])

# This was discovered by performing Gaussian Elimination on the discovered keystream
# There is a generalised algo for solving Guassian Elimination that could have produced
# this function in an automated way
def lfsr(init_vector):
    registers = list(bin(init_vector).lstrip("-0b").zfill(6)[-6:])
    while True:
        registers.insert(0, "1" if registers[-1] != registers[-2] else "0")
        yield registers.pop()

def xor_bitstream(a, b):
    return "".join(["1" if a != b else "0" for a, b in zip(a, b)])

def apply_keystream(lfsr_init_vector, text):
    return bitdecode(xor_bitstream(lfsr(lfsr_init_vector), bitencode(text)))

def print_ciphertext_and_chosen_plaintext(ciphertext, chosen_plaintext):
    print "\n==========="
    print "Ciphertext:"
    print "===========\n"
    print ciphertext
    print "\n================="
    print "Chosen Plaintext:"
    print "=================\n"
    print chosen_plaintext

def print_keystream(keystream):
    print "\n==================="
    print "Revealed keystream:"
    print "===================\n"
    print keystream

def print_decrypted_message(plaintext):
    print "\n==================="
    print "Revealed plaintext:"
    print "===================\n"
    print plaintext, "\n"

if __name__ == "__main__":
    ciphertext = "j5a0edj2b"
    chosen_plaintext = "WPI"
    lfsr_init_vector = 63
    keystream = xor_bitstream(bitencode(ciphertext), bitencode(chosen_plaintext))
    plaintext = apply_keystream(lfsr_init_vector, ciphertext)
    print_ciphertext_and_chosen_plaintext(ciphertext, chosen_plaintext)
    print_keystream(keystream)
    print_decrypted_message(plaintext)

The code above can do everything except perform the Gauss-Jordan Elimination to find the coefficients. This I did by hand. However, since a general algorithm exists, then there’s no reason the code couldn’t be extended to perform the full attack.

The full plaintext is revealed as:

WPIWOMBAT

3. The wombat is an animal that lives in Tasmania and South-Eastern Australia.

4. We performed a known-plaintext attack.

Previous Exercise Next Exercise

Thomas Busby

I write about computing stuff