Understanding Cryptography by Christof Paar and Jan Pelzl - Chapter 2 Solutions - Ex2.8

Monday. 18 December 2017 - 6 mins

Exercise 2.8

In this problem we will study LFSRs in somewhat more detail. LFSRs come in three flavors:

LFSRs which generate a maximum-length sequence. These LFSRs are based on primitive polynomials.
LFSRs which do not generate a maximum-length sequence but whose sequence length is independent of the initial value of the register. These LFSRs are based on irreducible polynomials that are not primitive. Note that all primitive polynomials are also irreducible.
LFSRs which do not generate a maximum-length sequence and whose sequence length depends on the initial values of the register. These LFSRs are based on reducible polynomials.

We will study examples in the following. Determine all sequences generated by

$x^4 + x + 1$
$x^4 + x^2 + 1$
$x^4 + x^3 + x^2 + x + 1$

Draw the corresponding LFSR for each of the three polynomials. Which of the polynomials is primitive, which is only irreducible, and which one is reducible? Note that the lengths of all sequences generated by each of the LFSRs should add up to $2^m − 1$.

Solution

I haven’t yet verified this solution independently. If you spot any mistakes, please leave a comment in the Disqus box at the bottom of the page.

1. This LFSR derived from $x^4 + x + 1$ can be represented as follows:

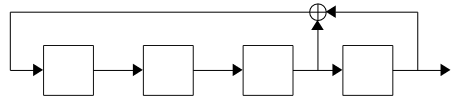
LFSR 1

Starting from $0001_2$, the LFSR will iterate through the following states:

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 0 & 0 & 0 & 1 & 1 \\ 2 & 1 & 0 & 0 & 0 & 0 \\ 3 & 0 & 1 & 0 & 0 & 0 \\ 4 & 0 & 0 & 1 & 0 & 0 \\ 5 & 1 & 0 & 0 & 1 & 1 \\ 6 & 1 & 1 & 0 & 0 & 0 \\ 7 & 0 & 1 & 1 & 0 & 0 \\ 8 & 1 & 0 & 1 & 1 & 1 \\ 9 & 0 & 1 & 0 & 1 & 1 \\ 10 & 1 & 0 & 1 & 0 & 0 \\ 11 & 1 & 1 & 0 & 1 & 1 \\ 12 & 1 & 1 & 1 & 0 & 0 \\ 13 & 1 & 1 & 1 & 1 & 1 \\ 14 & 0 & 1 & 1 & 1 & 1 \\ 15 & 0 & 0 & 1 & 1 & 1 \\ \hline & 0 & 0 & 0 & 1 & 1 \end{array}$

The polynomial produces a single $2^4 - 1$ length sequence of internal states (containing all non-zero 4-bit binary numbers) before repeating and is therefore a primitive polynomial.

2. This LFSR derived from $x^4 + x^2 + 1$ can be represented as follows:

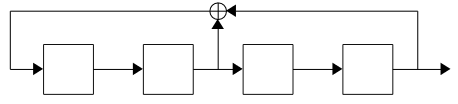
LFSR 2

Starting from $0001_2$, $1001_2$ and $0110_2$, the LFSR will iterate through the following states:

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 0 & 0 & 0 & 1 & 1 \\ 2 & 1 & 0 & 0 & 0 & 0 \\ 3 & 0 & 1 & 0 & 0 & 0 \\ 4 & 1 & 0 & 1 & 0 & 0 \\ 5 & 0 & 1 & 0 & 1 & 1 \\ 6 & 0 & 0 & 1 & 0 & 0 \\ \hline & 0 & 0 & 0 & 1 & 1 \end{array}$

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 1 & 0 & 0 & 1 & 1 \\ 2 & 1 & 1 & 0 & 0 & 0 \\ 3 & 1 & 1 & 1 & 0 & 0 \\ 4 & 1 & 1 & 1 & 1 & 1 \\ 5 & 0 & 1 & 1 & 1 & 1 \\ 6 & 0 & 0 & 1 & 1 & 1 \\ \hline & 1 & 0 & 0 & 1 & 1 \end{array}$

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 0 & 1 & 1 & 0 & 0 \\ 2 & 1 & 0 & 1 & 1 & 1 \\ 3 & 1 & 1 & 0 & 1 & 1 \\ \hline & 0 & 1 & 1 & 0 & 0 \end{array}$

The polynomial produces three distinct sequences of internal states (together containing all non-zero 4-bit binary numbers) of varying lengths. It is therefore a reducible polynomial.

2. This LFSR derived from $x^4 + x^3 + x^2 + x + 1$ can be represented as follows:

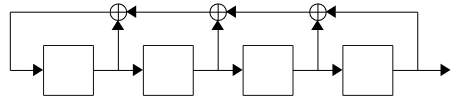
LFSR 3

Starting from $0001_2$, $1111_2$ and $1001_2$, the LFSR will iterate through the following states:

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 0 & 0 & 0 & 1 & 1 \\ 2 & 1 & 0 & 0 & 0 & 0 \\ 3 & 1 & 1 & 0 & 0 & 0 \\ 4 & 0 & 1 & 1 & 0 & 0 \\ 5 & 0 & 0 & 1 & 1 & 1 \\\hline & 0 & 0 & 0 & 1 & 1 \end{array}$

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 1 & 1 & 1 & 1 & 1 \\ 2 & 0 & 1 & 1 & 1 & 1 \\ 3 & 1 & 0 & 1 & 1 & 1 \\ 4 & 1 & 1 & 0 & 1 & 1 \\ 5 & 1 & 1 & 1 & 0 & 0 \\\hline & 1 & 1 & 1 & 1 & 1 \end{array}$

$\begin{array}{c|c c c c|c} & s_3 & s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 1 & 0 & 0 & 1 & 1 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 3 & 1 & 0 & 1 & 0 & 0 \\ 4 & 0 & 1 & 0 & 1 & 1 \\ 5 & 0 & 0 & 1 & 0 & 0 \\\hline & 1 & 0 & 0 & 1 & 1 \end{array}$

The polynomial produces three distinct sequences of internal states (together containing all non-zero 4-bit binary numbers) of the same length. It is therefore an ireducible (but not primitive) polynomial.

Previous Exercise Next Exercise

Thomas Busby

I write about computing stuff