Understanding Cryptography by Christof Paar and Jan Pelzl - Chapter 2 Solutions - Ex2.5

Monday. 18 December 2017 - 2 mins

Exercise 2.5

We will now analyze a pseudorandom number sequence generated by a LFSR characterized by $(c_2 = 1, c_1 = 0, c_0 = 1)$.

What is the sequence generated from the initialization vector $(s_2 = 1, s_1 = 0, s_0 = 0)$?
What is the sequence generated from the initialization vector $(s_2 = 0, s_1 = 1, s_0 = 1)$?
How are the two sequences related?

Solution

This solution is verified as correct by the official Solutions for Odd-Numbered Questions manual.

This LFSR can be visualised as such:

LFSR

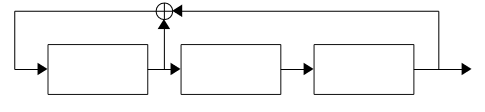
1. The sequence generated by $(s_2 = 1, s_1 = 0, s_0 = 0)$ is as follows:

$\begin{array}{c c c|c} s_2 & s_1 & s_0 & \text{Output} \\ \hline 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ \hline 1 & 0 & 0 & 0 \end{array}$

Note: the final row is the same as the first, meaning it will loop infinitely.

2. The sequence generated by $(s_2 = 0, s_1 = 1, s_0 = 1)$ is as follows:

$\begin{array}{c c c|c} s_2 & s_1 & s_0 & \text{Output} \\ \hline 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ \hline 0 & 1 & 1 & 1 \end{array}$

Note: the final row is the same as the first, meaning it will loop infinitely.

3. Since $(0, 1, 1)$ is part of the sequence for $(1, 0, 0)$, its loop is exactly the same, but rotated back by three positions. Both of them give the same loop of states (which contains of all non-zero 3-bit binary numbers), but starting from whatever was chosen to initialise it.

Previous Exercise Next Exercise

Thomas Busby

I write about computing stuff